Alpha Beta Pruning

The disadvantage of the minimax algorithm is that all nodes in the game tree cut off to a certain depth were examined.

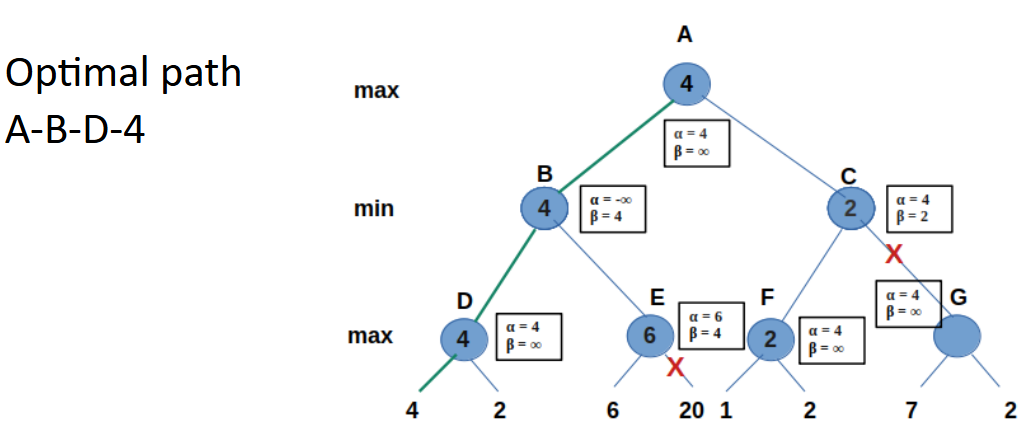
Alpha-beta pruning reduces the number of nodes explored.

Key Points

Game trees can be enormous.
Some branches have no effect.
Several branches can be removed.
Pruning the branches reduces the time for the minimax algorithm.

Alpha & Beta Variables

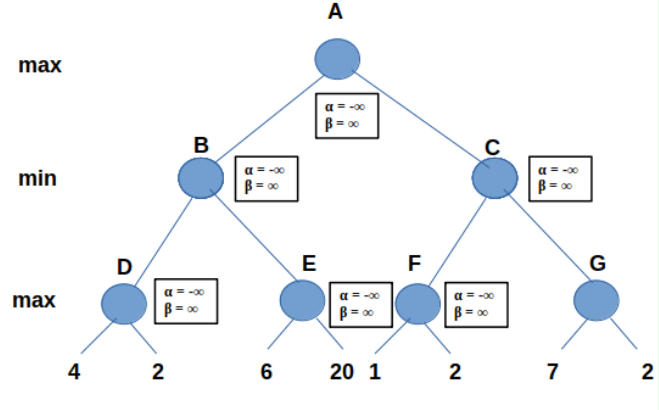
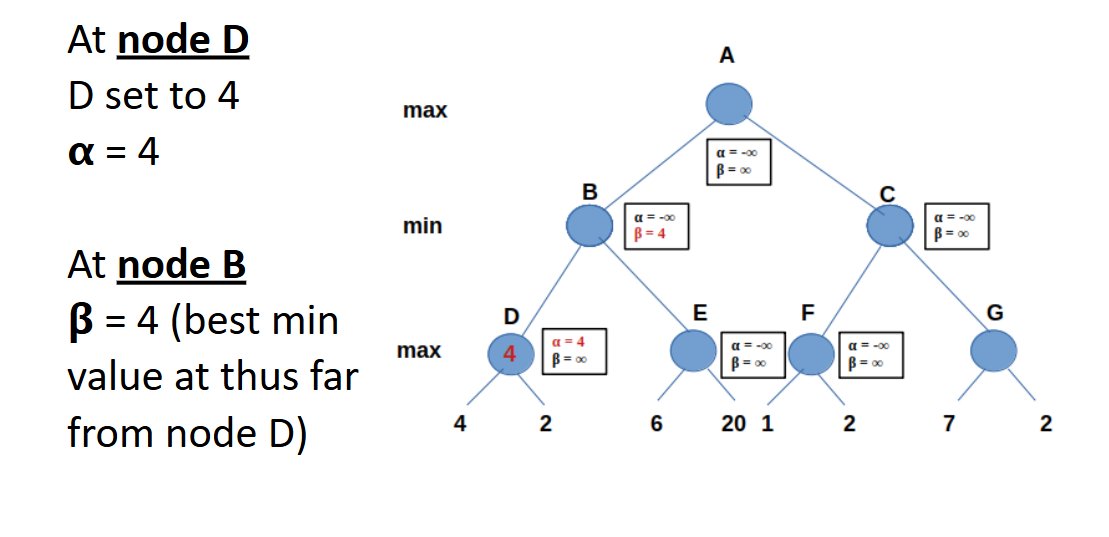
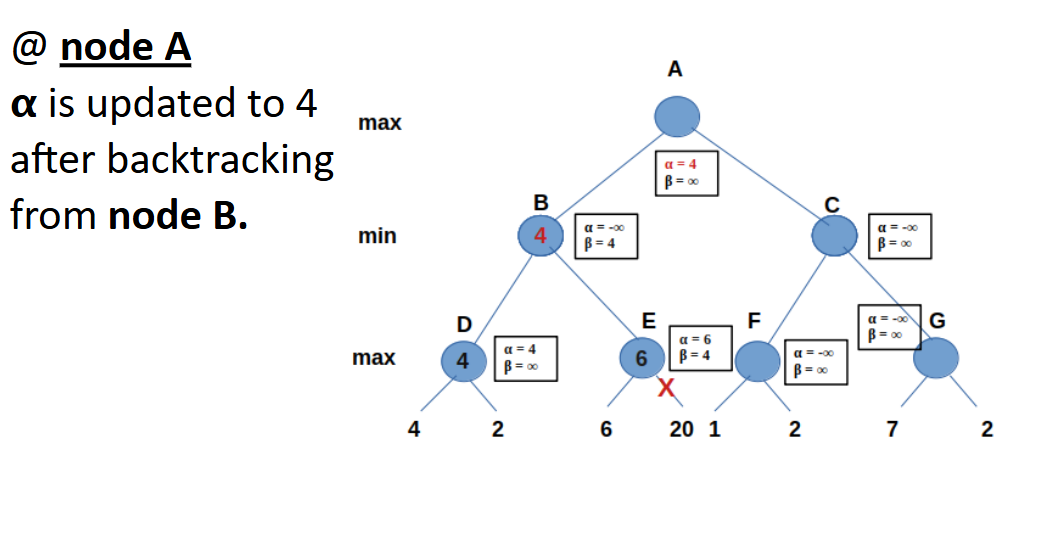
Two extra variables are assigned to every node in the tree: alpha (α) and beta (β).

ALPHA (α)

Stores the best already explored option along a path to the root for the max layer.
Represents the maximum score the maximizer can receive.
Only the maximizer can change this value.
Initial value: -∞ (negative infinity).

BETA (β)

Stores the best already explored option along a path to the root for the minimizing layer.
Represents the minimum score the maximizer can receive.
Only the minimizer can change this value.
Initial value: ∞ (positive infinity).

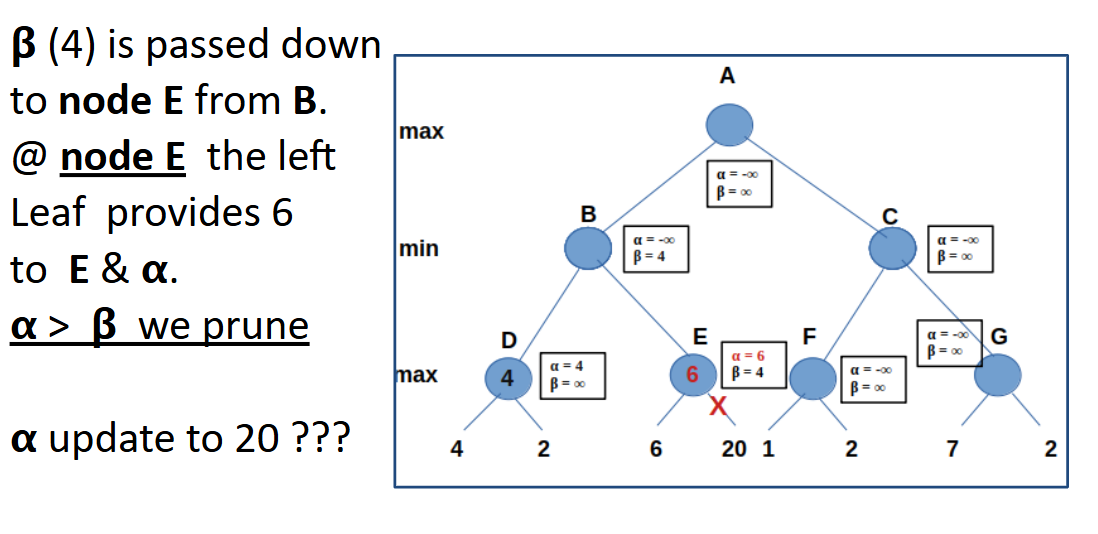
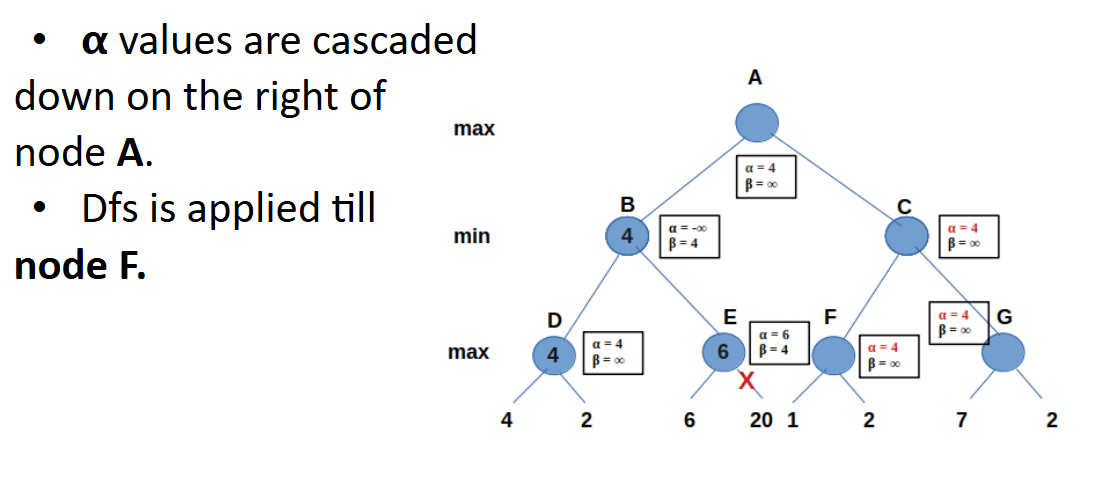
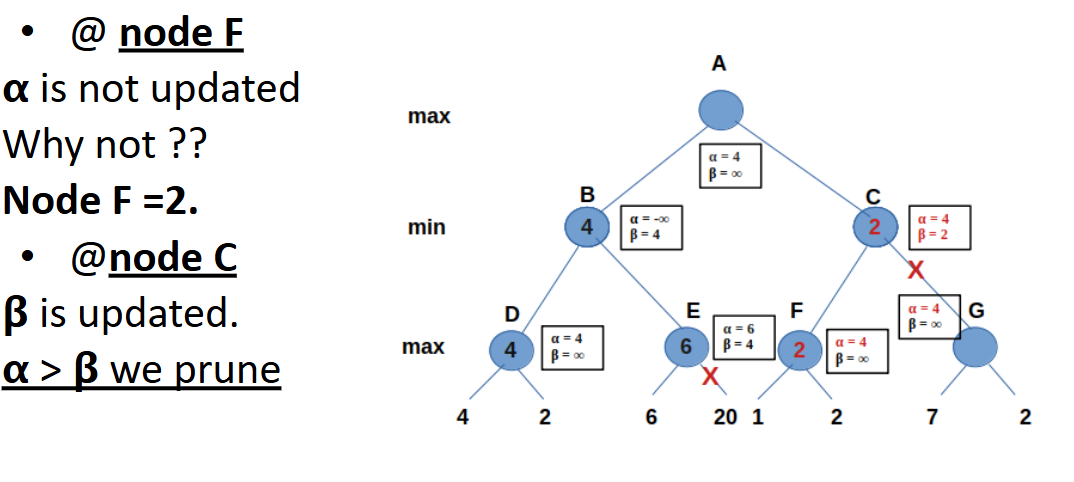
Pruning Condition

If α ≥ β, a given branch can be pruned, meaning there is no need to visit the given children.
Pruning is not always guaranteed—it depends on the distribution order of values.

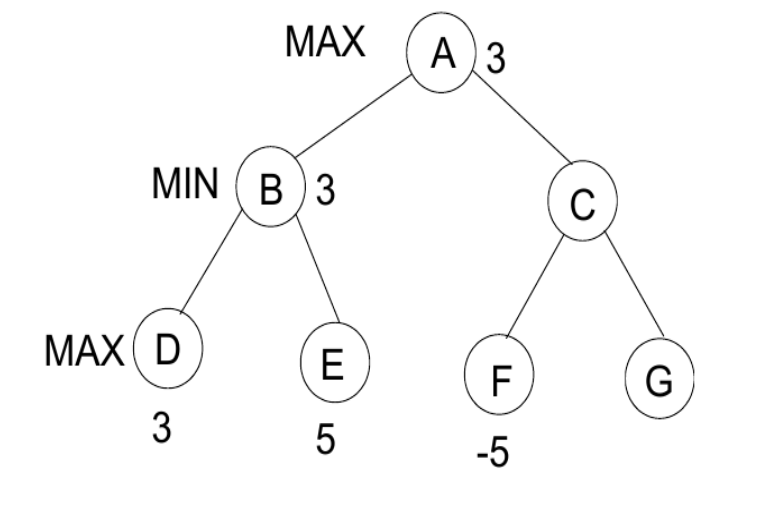
Sample 1

The children of B have static values of 3 and 5, and B is at the MIN level, so the value returned to B is 3.

If we consider F, it has a value of -5.

Thus, the value returned to C is at most -5. However, A is at a MAX level, meaning the value at A will be at least 3, which is greater than -5.

Regardless of the value of G, A has a value of 3. Therefore, we do not need to explore G because its value will not affect the value returned to A.

This is called the alpha cut.

Similarly, we can get a beta cut if the value of a subtree is always greater than the value returned by its sibling at a minimizing level.

In Alpha-Beta pruning, we assign two extra variables to every node in the search tree: alpha (α) and beta (β).